Aproksymacja jednostajna.
Dla funkcji f ( x ) określonej na przedziale < a; b > poszukujemy funkcji F (x) dającej najmniejsze maksimum różnicy między F (x) a f (x) na całym przedziale < a; b >;
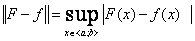(1)
Zanim dokonam bardziej szczegółowego omówienia pewnych typowych rodzajów aproksymacji, podam dwa sformułowane przez Weierstrassa twierdzenia, których dowody można znaleźć w podręcznikach [Acheizer N.I.1957] oraz [Ralston A.1975]
Tw.1. Jeżeli funkcja f jest ciągła na skończonym przedziale <a; b>, to dla każdego 
dodatniego można dobrać takie n, że jest możliwe utworzenie wielomianu 
stopnia n (n= n() ) , który spełnia nierówność [2]
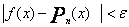
na całym przedziale < a; b >, tzn. dla wszystkich punktów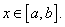 
Tw.2. Jeżeli funkcja f jest funkcją ciągłą na R okresową o okresie 2
, to dla każdego dodatniego istnieje wielomian trygonometryczny
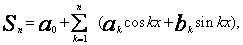n = n()
spełniający dla wszystkich x nierówność
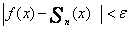
Twierdzenie 1 jest dodatkowym argumentem na poparcie aproksymacji wielomianowych, gdyż gwarantuje ono, że zawsze można znaleźć wielomian o dowolnie małym odchyleniu od funkcji f na przedziale < a; b >.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.