www.eprace.edu.pl » aproksymacja-wielomianami » Aproksymacja średniokwadratowa.

Aproksymacja średniokwadratowa.

Niech w przestrzeni liniowej z iloczynem skalarnym dany będzie element f oraz ortonormalny układ elementów 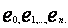, tzn. iloczyny skalarne 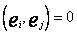dla

oraz 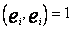dla

Tw.1

Liczby

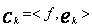, k = 0,1,...,n (2)

nazywają się współczynnikami Fouriera elementu f względem układu .[3]

Tw.2 Element

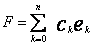, (3)

gdzie liczby określone są wzorami (2), jest elementem optymalnym, tj.

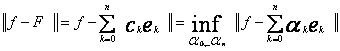(4)

Dla współczynników Fouriera zachodzi nierówność Bessela

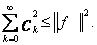(5)

(tzn. w przestrzeni liniowej z iloczynem skalarnym).

W przestrzeni Hilberta zamiast nierówności Bessela otrzymujemy równość Persevala

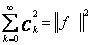, (6)

którą można rozważać jako uogólnienie twierdzenia Pitagorasa.

Ponieważ z każdego układu ortogonalnego bardzo łatwo otrzymać układ ortonormalny, to wymaganie ortonormalności układu nie zmniejsza ogólności rozważań. Wszystkie wyniki tego podpunktu łatwo parafrazować w terminach układów ortogonalnych, zwłaszcza w terminach ortogonalnych układów funkcji.

czytaj dalej: Aproksymacja trygonometryczna »