Aproksymacja interpolacyjna a aproksymacja jednostajna
Różnica podstawowa między zagadnienia interpolacji i zagadnieniem aproksymacji polega na tym, że w przypadku interpolacji funkcja f (x) w punktach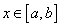 
różnych od węzłów interpolacji nie jest znana. Bez dodatkowych założeń o zachowaniu tej funkcji w przedziale 
oszacowanie błędu interpolacji w punktach nie będących węzłami interpolacji nie jest możliwe. W przypadku aproksymacji funkcja f jest znana, można oszacować różnicę 
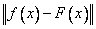i na podstawie takiego oszacowania można wyciągnąć odpowiednie wnioski o możliwym zachowaniu rozwiązania zagadnienia interpolacji i o możliwych problemach powstających przy rozwiązaniu takiego zagadnienia. [ Fortuna Z. 2001]
Zacznę od oszacowania dokładności aproksymacji wielomianem interpolacyjnym Taylora. Założę, że w rozpatrywanym przedziale istnieją nie tylko pochodne funkcji f (x) do rzędu n, ale do rzędu n + 1 włącznie, i wprowadzam normę
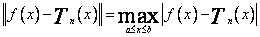(69)
Oszacowanie błędu aproksymacji
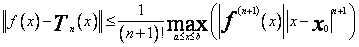(70)
jest konsekwencją reszty wzoru Taylora w postaci Lagrange`a
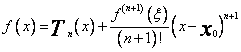(71)
gdzie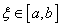 
Ponieważ wybór punktu 
należącego do danego przedziału nie jest ściśle określony, więc powstaje pytanie najbardziej racjonalnego wyboru węzła aproksymacji. Błąd aproksymacji Taylora będzie najmniejszy, jeśli węzeł jest środkiem przedziału
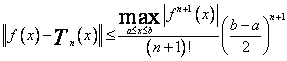(72)
Dla aproksymacji interpolacyjnej za pomocą wzorów interpolacyjnych Newtona mamy następujące oszacowanie błędu:
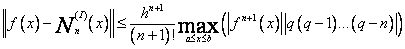(73)
oraz
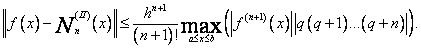(74)
Dla aproksymacji interpolacyjnej za pomocą wzorów Gaussa mamy:
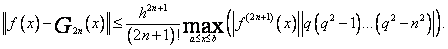(75)
Dla aproksymacji interpolacyjnej za pomocą wzoru Lagrange`a zachodzi następujące oszacowanie błędu:
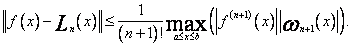(76)
Zajmiemy się minimalizacją prawej strony oszacowania (76) przez najlepszy wybór węzłów. Wielomian
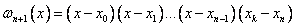ma współczynnik wiodący równy jedynce, a więc mamy
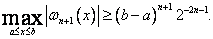
Jeśli jako węzły interpolacji przyjąć zera przekształconego wielomianu Czebyszewa pierwszego rodzaju
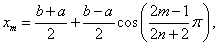m = 1,2,...n + 1,
to wtedy
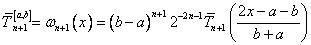
oraz
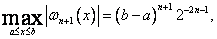
a więc przy takim wyborze węzłów mamy najlepsze oszacowanie
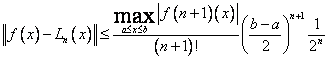. (77)
Porównam jeszcze oszacowania błędów aproksymacji Taylora (72) i aproksymacji Lagrange`a (77) z węzłami będącymi zerami odpowiedniego wielomianu Czebyszewa pierwszego rodzaju. Ze wzorów (72) i (77) wynika, że dokładność wielomianu Taylora jest 
razy mniejsza od dokładności odpowiedniego wielomianu Lagrange`a. [Fortuna Z. 2001].
Przypuśćmy, że w przedziale [ a, b ] mamy ciąg węzłów
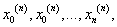n = 0,1,2,...
i ciąg odpowiednich wielomianów interpolacyjnych Lagrange`a aproksymujących funkcję f (x). Nasuwa się pytanie: jak zachowuje się błąd aproksymacji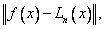 
gdy 
?
Przykład 13.
Na rysunkach 4.1a i 4.1b podano wykresy funkcji
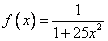
i jej wielomianów interpolacyjnych Lagrange`a 
i 
opartych na węzłach wielomianów równoodległych w przedziale [ -1, 1 ]. W końcach przedziału sytuacja będzie tylko pogarszała się ze wzrostem n , natomiast w środkowych punktach przedziału aproksymacja może być dobra.
Przykład 14.
Na rysunkach 4.2a i 4.2b podano wykresy tej samej funkcji w przedziale [ -1, 1 ] i jej wielomianów interpolacyjnych Lagrange`a i opartych na zerach odpowiednich wielomianów Czebyszewa 
i 
.
Widać wyraźnie, że w przypadku węzłów równoodległych mamy do czynienia ze zjawiskiem Rungego, natomiast w przypadku aproksymacji za pomocą wielomianu Lagrange`a z węzłami Czebyszewa błąd aproksymacji jest znacznie mniejszy.
Nie oznacza to jednak, że aproksymacja za pomocą wielomianu Lagrange`a nawet z węzłami Czebyszewa zawsze jest zbieżna do funkcji f (x) przy . Dla analizy takiej zbieżności przytoczę kilka niezbędnych twierdzeń.
Twierdzenie 1. (Weierstrassa) Jeśli funkcja f (x) jest ciągła w przedziale [ a, b ], to dla dowolnej liczby 
istnieje taki wielomian algebraiczny
,
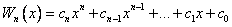że dla wszystkich wartości x z rozważanego przedziału [ a, b ] jednostajnie będzie spełniona nierówność
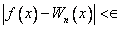
Przykładem takiego wielomianu 
jest wielomian Bernsteina funkcji f (x) określonej w przedziale 
[11]
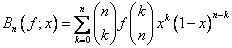(78)
Można udowodnić, że dla funkcji ciągłej f (x)
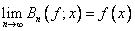(79)
jednostajnie w przedziale [ a, b ].
Z twierdzenia Weierstrassa wynika następujące twierdzenie.
Twierdzenie 2 ("optymistyczne") Dla dowolnej funkcji f (x) ciągłej w przedziale [ a, b ] istnieje ciąg wielomianów interpolacyjnych zbieżnych jednostajnie do f (x) w tym przedziale.[ Fortuna Z. 2001 ].
Twierdzenia 1 i 2 w pewnym sensie usprawiedliwiają aproksymację wielomianową, gdyż dają gwarancję, że istnieje wielomian interpolacyjny aproksymujący funkcję f jednostajnie w przedziale [ a, b ]. Ale jest to tylko pozorne, że wielomian interpolacyjny Bernsteina jest rozwiązaniem zagadnienia aproksymacji jednostajnej. Celem aproksymacji jest znalezienie takiego wielomianu , który minimalizuje błąd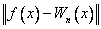 
. Wielomian Bernsteina 
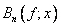stopnia n nie jest takim wielomianem. Wybór węzłów 
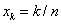nie jest najlepszy. Może zdarzyć się, że dla otrzymania potrzebnej dokładności , stopień n aproksymującego wielomianu Bernsteina 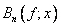będzie bardzo duży ( na przykład trzeba wziąć 
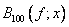, aby otrzymać 
), a tę samą dokładność aproksymacji można uzyskać korzystając z wielomianu interpolacyjnego Lagrange`a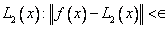 
. Wielomiany Bernsteina, chociaż prowadzą do konstruktywnego dowodu twierdzenia Weierstrassa, na ogół są nieprzydatne jako wielomiany aproksymujące.
Twierdzenie 3 (Fabera) ("pesymistyczne") Dla dowolnego układu węzłów interpolacyjnych istnieje funkcja ciągła f (x), do której ciąg jej wielomianów interpolacyjnych Lagrange`a 
nie jest jednostajnie zbieżny.
Twierdzenie 4 ("optymistyczne") Jeśli pochodna funkcji f jest ograniczona w przedziale [ a, b ], to ciąg jej wielomianów interpolacyjnych opartych na zerach odpowiednich wielomianów Czebyszewa pierwszego rodzaju jest w tym przedziale zbieżny jednostajnie do funkcji f.[12]
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.