Aproksymacja średniokwadratowa funkcji ciągłych
Przyjmijmy, że daną funkcję f (x) ciągłą na przedziale < a ; b > mamy aproksymować funkcję postaci
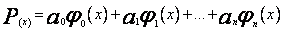
gdzie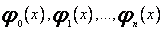 
są elementami bazy pewnej podprzestrzeni funkcji całkowalnych z kwadratem na przedziale < a; b >. Podobnie jak w przypadku, gdy f (x) była określona na dyskretnym zbiorze punktów, aproksymacja średniokwadratowa funkcji ciągłych polega na znalezieniu takiego ciągu współczynników 
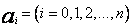, aby otrzymać minimum normy.[10] Przyjąłem zatem, tak jak w przypadku aproksymacji dyskretnej, że funkcja wagowa jest stała i równa jedności
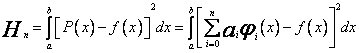(64)
Jak poprzednio, aby rozwiązać zadanie obliczam pochodne cząstkowe
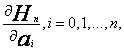przyrównuję je do zera i z otrzymanego układu równań wyznaczam współczynniki 
.
Przykład 11.
Znaleźć przybliżenie funkcji f (x) = sin x na przedziale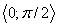 
wielomianem stopnia co najwyżej drugiego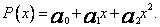 
Układ równań ma postać
,
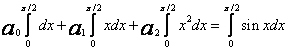
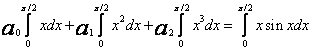
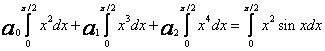czyli
,
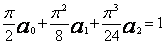
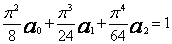
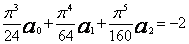Rozwiązaniem powyższego układu są liczby
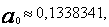
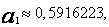
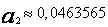
Zatem
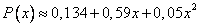
Obliczam średni błąd aproksymacji
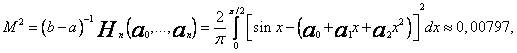czyli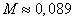 
Rachunki będą znacznie prostsze, jeżeli zamiast ciągu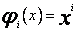 
użyję ciągu funkcji ortogonalnych z wagą. Może to być na przykład omówiony wcześniej ciąg Legendre`a
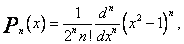n = 0,1,2,... (65)
Przykład 12.
Aproksymować funkcję z poprzedniego przykładu posługując się wielomianami Legendre`a.
Ponieważ na przedziale < -1, 1 > wielomiany Legendre`a tworzą ciąg ortogonalny z wagą 1, a funkcja f (x) = sin x mam aproksymować na przedziale 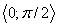, wprowadzam nową zmienną
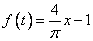(66)
której wartości należą do przedziału 
dla 
. Aproksymować będę zatem funkcję
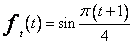
wielomianem
,
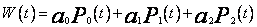gdzie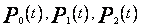 
są wielomianami Legendre`a.
Odpowiednie współczynniki wynoszą
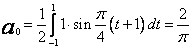
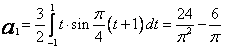
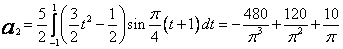
Zatem
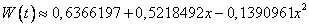
Średni błąd aproksymacji
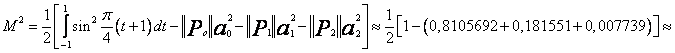
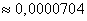
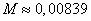
Jak widać, wskutek użycia do aproksymacji wielomianów ortogonalnych uzyskałem ponad dziesięciokrotne zmniejszenie średniego błędu aproksymacji.
Do aproksymacji używa się także układów funkcji ortogonalnych z wagą w (x) będącą daną, dodatnią funkcją na przedziale < a; b >. Warunek ortogonalności ma wówczas postać
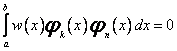dla 
(67)
a w wielomianie uogólnionym dobieramy współczynniki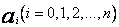 
tak, aby norma była najmniejsza dla danego ustalonego n .
Przykładem ortogonalnego układu funkcji z wagą na przedziale < -1;1 > są wielomiany Czebyszewa (wzór 19) z funkcją wagową
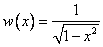, (68)
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.