
Aproksymacja wielomianami Czebyszewa pierwszego rodzaju
Zagadnienie to zostało sformułowane przez rosyjskiego matematyka P.L. Czebyszewa jako zagadnienie znajdowania wielomianu algebraicznego najlepiej przybliżającego zero na zadanym przedziale. Aby można je było rozwiązać ,skorzystajmy z wielomianów Czebyszewa pierwszego rodzaju![]()
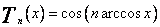 [ Fortuna Z. " Metody numeryczne ", W - wa, WNT 2001, str. 36.]
[ Fortuna Z. " Metody numeryczne ", W - wa, WNT 2001, str. 36.]
Funkcję f (x) z przestrzeni ![]() z wagą
z wagą 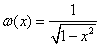 aproksymujemy jej sumą Fouriera
aproksymujemy jej sumą Fouriera

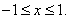 (19)
(19)
Współczynniki ![]() obliczamy za pomocą wzorów
obliczamy za pomocą wzorów
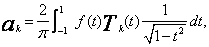 k = 0,1,2,...,n. (20)
k = 0,1,2,...,n. (20)
Zachodzi równość
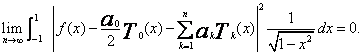 (21)
(21)
Tw. 1.
Jeśli funkcja f (x) ma w przedziale ![]() trzecią pochodną ciągłą, to jest ona w tym przedziale rozwijalna w szereg jednostajnie zbieżny według układu wielomianów Czebyszewa pierwszego rodzaju.
trzecią pochodną ciągłą, to jest ona w tym przedziale rozwijalna w szereg jednostajnie zbieżny według układu wielomianów Czebyszewa pierwszego rodzaju.
Przykład 3. Obliczyć kilka współczynników aproksymacji funkcji ![]() w przedziale
w przedziale ![]() wielomianami Czebyszewa pierwszego rodzaju.
wielomianami Czebyszewa pierwszego rodzaju.
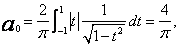
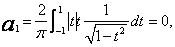
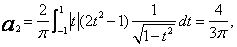 (22)
(22)
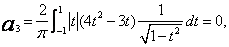
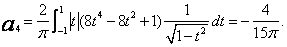
komentarze
skomentowano: 2017-05-15 19:37:35 przez: Basha
Copyright © 2008-2010 EPrace oraz autorzy prac.