
Aproksymacja za pomocą wielomianów ortogonalnych
Jak wykazałem w poprzednim punkcie, przy aproksymacji wielomianowej z funkcjami bazowymi ze wzrostem stopnia wielomianu obliczenia stają się coraz bardziej pracochłonne, a ponadto ich wyniki są niepewne. Oczywiście gdy do obliczeń wykorzystujemy maszynę cyfrową, dokładność wyników możemy w jakimś stopniu poprawić, na przykład przez zwiększenie liczby cyfr znaczących, lecz i ten sposób ma ograniczony zakres. Dodatkową trudnością jest fakt, że zmiana stopnia wielomianu przybliżającego wymaga ponownego rozwiązania układu normalnego, co też przemawia przeciwko stosowaniu ciągu funkcji 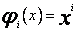 do aproksymacji. Obydwie te trudności można usunąć używając do aproksymacji wielomianów ortogonalnych[9]
do aproksymacji. Obydwie te trudności można usunąć używając do aproksymacji wielomianów ortogonalnych[9]
W punkcie tym omówimy problem aproksymacji za pomocą funkcji określonych na dyskretnym zbiorze punktów, a następnie aproksymację funkcji ciągłych.
Zdefiniuję zatem ortogonalność funkcji na dyskretnym zbiorze punktów.
Def. Funkcję f (x) i g (x) nazywamy ortogonalnymi na dyskretnym zbiorze punktów 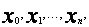 jeśli
jeśli
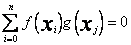 , (48)
, (48)
przy czym
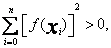
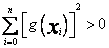
Analogicznie, ciąg funkcyjny
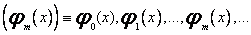 (49)
(49)
nazywamy ortogonalnym na zbiorze punktów 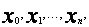 jeśli
jeśli
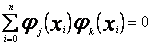
![]() dla
dla ![]() (50)
(50)
Zakładamy, że nie wszystkie punkty ![]() są miejscami zerowymi rozpatrywanych funkcji
są miejscami zerowymi rozpatrywanych funkcji 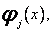 tzn.
tzn. 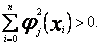
Zastosowanie do aproksymacji wielomianów ortogonalnych usuwa jedną z podstawowych trudności obliczeniowych pojawiających się przy aproksymacji wielomianami algebraicznymi - złe uwarunkowanie macierzy układu normalnego. Przy aproksymacji wielomianami ortogonalnymi macierz układu normalnego jest macierzą diagonalną, a jej elementy położone na głównej przekątnej wynoszą
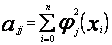
Załóżmy, że mamy n + 1 równoodległych punktów 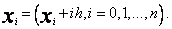
Za pomocą przekształcenia liniowego
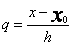
przeprowadzę te punkty odpowiednio w kolejne liczby całkowite od 0 do n.
Poszukuję ciągu wielomianów
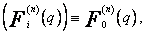
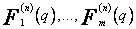 (51)
(51)
(dolny indeks oznacza stopień, ![]() ) spełniający na zbiorze punktów q = 0,1,...,n warunek ortogonalności
) spełniający na zbiorze punktów q = 0,1,...,n warunek ortogonalności
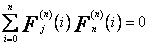 , dla
, dla ![]() , (52)
, (52)
przy czym
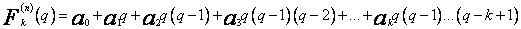 (53)
(53)
W celu uproszczenia zapisu można użyć tutaj wprowadzonego pojęcia wielomianu czynnikowego
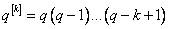
Wówczas
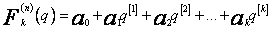 (54)
(54)
Często używa się unormowanego ciągu wielomianów (51), spełniających warunek
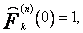 k = 0,1,...,m
k = 0,1,...,m
(55)
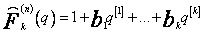
Po stosunkowo łatwych przekształceniach ([Demidowicz B.L. 1965], [Ralston A.1975]), otrzymujemy związek
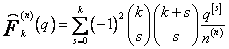 , (56)
, (56)
k = 0,1,2,...,m ,
gdzie ![]() są symbolami Newtona. Wzór (56) określa wielomiany Grama stopni k = 0,1,2,...m dla n + 1 równoodległych węzłów.
są symbolami Newtona. Wzór (56) określa wielomiany Grama stopni k = 0,1,2,...m dla n + 1 równoodległych węzłów.
Wzór aproksymacyjny oparty na wielomianach Grama, będący odpowiednikiem wzoru
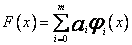 , (57)
, (57)
ma postać
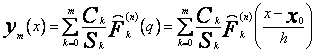 (58)
(58)
dla ![]() , gdzie
, gdzie
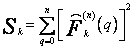
(59)
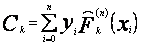
Przykład 10.
Dana jest tablica wartości funkcji f (x) ( tabl. 3 ). Znaleźć najlepszy, w sensie aproksymacji średniokwadratowej, wielomian przybliżający funkcję f (x).
Tabl.3
| x | 1 | 1.5 | 2 | 2.5 | 3 |
| y | 3 | 4.75 | 7 | 9.75 | 13 |
Żródło: [ Fortuna Z. " Metody numeryczne ", W- wa, WNT 2001.]
Ponieważ węzły są równoodległe, posłużę się wielomianami Grama. Konstruuję wielomian aproksymacyjny dla n = 4. Wartości 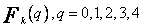 obliczam ze wzoru (57)
obliczam ze wzoru (57)
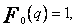
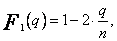
![]()
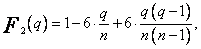
![]()
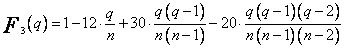 ,
, ![]()
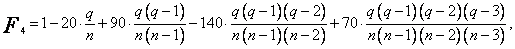
![]()
i zestawiam w postaci tablicy (tabl.4). Korzystając następnie ze wzorów (59), obliczam wartości ![]() i
i ![]() oraz
oraz 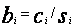 (tabl.5) i ze wzoru (57) otrzymujemy dla
(tabl.5) i ze wzoru (57) otrzymujemy dla
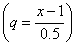
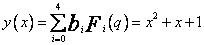
Tabl.4
| q | 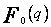 | 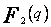 | 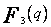 | 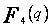 | |||
| 0
1 2 3 4 | 1
1.5 2 2.5 3 | 3
4.75 7 9.75 13 | 1
1 1 1 1 | 1
0.5 0 -0.5 -1 | 1
-0.5 -1 -0.5 1 | 1
-2 0 2 -1 | 1
-4 6 -4 1 |
Źródło: [ Fortuna Z., " Metody numeryczne ", W - wa, WNT 2001.]
Tabl.5
| 37.5 | -12.5 | 1.75 | 0 | 0 | |
| 5
7.5 | 2.5
-5 | 3.5
0.5 | 10
0 | 70
0 |
Źródło: [ Fortuna Z. " Metody numeryczne ", W wa, WNT 2001.]
Jeżeli punkty, w których są dane wartości funkcji nie są równoodległe, to korzystamy z pewnych związków rekurencyjnych. Niech mianowicie 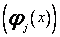 będzie dowolnym ciągiem wielomianów ortogonalnych na zbiorze punktów
będzie dowolnym ciągiem wielomianów ortogonalnych na zbiorze punktów ![]() . Można udowodnić ( np. indukcyjnie ), że zachodzi związek
. Można udowodnić ( np. indukcyjnie ), że zachodzi związek
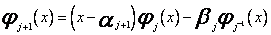 dla j = 0,1,... (60)
dla j = 0,1,... (60)
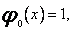
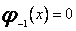 ,
,
gdzie stałe ![]() i
i ![]() są określone wzorami
są określone wzorami
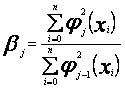
(61)
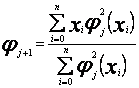
Odpowiednikami wzorów (58) i (59) są teraz
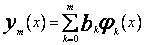 (62)
(62)
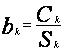
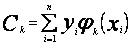 (63)
(63)
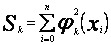
komentarze
Dziękuję za w miarę jasne przedstawienie problemu dla niefachowca
skomentowano: 2011-05-10 08:53:04 przez: Paweł
Gorszego zamotania indeksów to jeszcze nie widziałem. Pozdro dla autora.
skomentowano: 2012-10-15 09:06:46 przez: gosc z polibudy
skomentowano: 2019-12-06 18:50:06 przez: Andrzej
skomentowano: 2022-05-13 10:36:55 przez:
Copyright © 2008-2010 EPrace oraz autorzy prac.