www.eprace.edu.pl » aproksymacja-wielomianami » Aproksymacja średniokwadratowa. » Aproksymacja wielomianowa

Aproksymacja wielomianowa

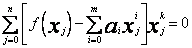(35)

k = 0,1,2,...m

Zmieniając kolejność sumowania, mamy

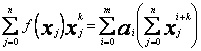(36)

k = 0,1,2,...m

i oznaczając

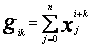(37)

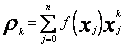
otrzymamy układ normalny (35) postaci

, k = 0,1,2,...,m (38)

Można wykazać, że jeżeli punkty 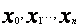są różne i , to wyznacznik układu (38) jest różny od zera, a więc układ ten ma jednoznaczne rozwiązanie. Jeżeli m = n, to wielomian aproksymacyjny F(x) pokrywa się z wielomianem interpolacyjnym dla punktów .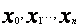

W praktyce stopień wielomianu jest, i powinien być, znacznie mniejszy od liczby punktów 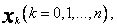wtedy bowiem korzystamy z dużej ilości informacji (np. wyników pomiarów) uzyskując równocześnie prostsze (niskiego stopnia) funkcje aproksymujące.

Przykład 7.

Niech dane będą wyniki pomiarów zestawione w tablicy 1. Poszukujemy zależności między x i y postaci

ax+ by=1 (39)

przy czym zadanie polega na znalezieniu " najlepszych" współczynników a oraz b.

Tabl.1

X	1	3	4	6	8	9	11	14
Y	1	2	4	4	5	7	8	9

Źródło: [ Fortuna Z. " Metody numeryczne ", W - wa, WNT 2001.]

Przy tak sformułowanym zadaniu pojawia się problem: czy rozpatrywać odchylenia x, czy y? Rozpatrzę obydwa przypadki, pokazując jednocześnie, że prowadzą one do różnych wyników.

Gdy przyjmiemy, że wartości y są obarczone pewnymi błędami, wówczas minimalizujemy wyrażenie

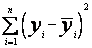, (40)

gdzie są określone za pomocą wzoru (40) dla i = 1,2,...,n. Jeżeli natomiast przyjmiemy, że wartości x są obarczone błędami, to powinniśmy minimalizować wyrażenie

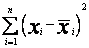(41)

przy czym

i = 1,2,...,n

Wartości i są każdorazowo brane z tablicy 1. Możliwe jest także, ale stosunkowo trudne, rozpatrywanie przypadku, gdy zarówno wartości x i y są obarczone błędami.

W przypadku minimalizacji wyrażenia (40) otrzymujemy układ normalny postaci

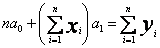
(42)

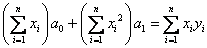
w którym 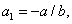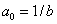i stąd

(43)

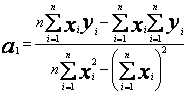
Układ normalny (42) dla danych z tablicy 1 ma rozwiązanie

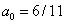i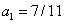

i stąd równanie (39) ma postać

11y - 7x= 6 (44)

Minimalizując w taki sposób wyrażenie (41), otrzymamy równanie

2x - 3y= -1 (45)

Jak widać, równania (44) i (45) są różne, chociaż ich wykresy prawie się pokrywają.

Wielomian aproksymujący daną funkcję f w sensie najmniejszych kwadratów powinien mieć stopień na tyle wysoki, aby dostatecznie przybliżać aproksymowaną funkcję, a jednocześnie stopień ten powinien być wystarczająco niski, aby wielomian ten wygładzał losowe błędy wynikające np. z pomiarów. W praktyce stopień wielomianu określamy a priori na podstawie analizy modelu fizycznego badanego zjawiska bądź też przeprowadzamy aproksymację kolejno wielomianami coraz to wyższych stopni. Proces ten prowadzimy tak długo, jak długo ze wzrostem stopnia wielomianu. Niestety, ta ostatnia metoda ma istotną wadę. Wiadomo, że dla wartości układ (38) jest układem źle uwarunkowanym, wskutek czego otrzymane wyniki obliczeń na maszynach cyfrowych mogą być tak bardzo zaburzone, iż nie nadają się do praktycznego wykorzystania przy aproksymacji.[7]

Aby wyjaśnić problem złego uwarunkowania macierzy współczynników układu (38), rozpatrzę następujący przykład. Niech wszystkie punkty będą rozłożone w jednakowych odstępach w przedziale <0;1>. Liczby , określone wzorem (37), można dla dużych wartości m przybliżyć następująco

(46)

i, k = 0,1,2,...,m

Macierz współczynników układu (38), po podzieleniu przez m, możemy przybliżyć macierzą

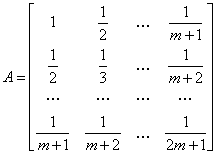(47)

Macierz odwrotna dla ma elementy rzędu co najmniej , co powoduje, że przy rozwiązywaniu układu (47) błędy zaokrągleń są tak duże, iż wyniki praktycznie tracą sens.

Powyższy przykład przemawia przeciwko stosowaniu aproksymacji z funkcjami bazowymi typu jednomianów z wyjątkiem przypadków, gdy m jest bardzo małe.

Przykład 8.

Aby zilustrować kłopoty w przypadku aproksymacji wielomianami wyższych stopni rozpatrzę następujący przykład. W tablicy 2 zestawiłem wartości zmiennych x i y (zostały one wygenerowane jako tablica wartości wielomianu)

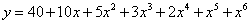
Tabl.2

x	y	x	y
1 2 3 4 5 6 7	62 232 1330 5984 20590 57952 140642	8 9 10 11 12 13 14	305080 606334 1123640 1966642 3282352 5262830 8153584

Źródło: [ Fortuna Z., " Metody numeryczne ", 2001]

Współczynniki układu normalnego utworzonego na podstawie tablicy 2 zmieniają się od 14 aż do . Wielomian aproksymacyjny stopnia szóstego, otrzymany po rozwiązaniu na maszynie cyfrowej, ma postać

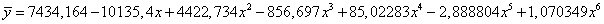
i jak widać bardzo się różni od wielomianu użytego do generowania danych. Różnice między wartościami y i dla x = 1,2,...,14 wynoszą od 48 do 886.

Gdy obliczenia będę wykonywał ze zwiększoną dokładnością, wówczas

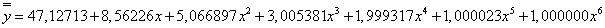
Ten wynik jest dużo lepszy, a różnice między y a mają wartości od zera do 5,7.

Aby można aproksymować wielomianami wyższych stopni, należy zastosować inną metodę rozwiązywania układu normalnego.

Innym sposobem umożliwiającym aproksymację wielomianami wyższych stopni jest zamiana bazy podprzestrzeni przez zastąpienie bazy jednomianów bazą złożoną z wielomianów ortogonalnych.[ Fortuna Z., " Metody numeryczne ", W - wa, WNT 2001, str. 82].

Przykład 9.

Napisać program na aproksymację wielomianem stopnia trzeciego dla n węzłów funkcji.

Układ normalny (38) ma postać

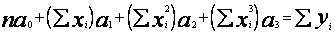
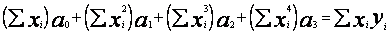
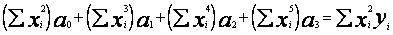
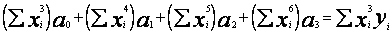
gdzie wszystkie sumowania są i =1 do i = n. Wprowadzę oznaczenia

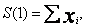
oraz

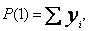
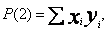
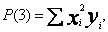
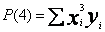
Program w pętli wczytuje kolejno punkt po punkcie ( x i y ) obliczając jednocześnie wartości wyrażeń S(1) do S(6) i P(1) do P(4). Po wczytaniu wszystkich n punktów zostaje zbudowana dwuwymiarowa tablica, będąca macierzą współczynników układu normalnego (TAB).

Następuje wywołanie procedury RUKL, która rozwiązuje układ umieszczając w tablicy A wartości pierwiastków będące szukanymi współczynnikami 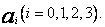Procedura RUKL może być dowolną procedurą rozwiązywania układu n równań liniowych z n niewiadomymi. Ponieważ macierz układu normalnego jest symetryczna ( i dodatnio określona), najbardziej efektywne byłyby procedury wykorzystujące metodę Cholesky`ego-Banachiewicza ( rozkładu 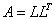) albo metodę rozkładu 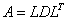, albo dowolna inna procedura wykorzystująca np. metodę eliminacji Gaussa. Procedury takie znajdują się w standardowej bibliotece programów każdej maszyny cyfrowej.[8]

PROGRAM APROKSYMACJA ;

VAR i, j, n, k: integer ;

x , y: real ;

TAB: ARRAY [ 1..4,1..5]OF real ;

A,P: ARRAY [1..4] OF real ;

S, SUMA: ARRAY [1..6] OF real ;

PROCEDURE RUKL ( we , wy: pointer; wymx, wymy: integer ) ;

...........

BEGIN {aproksymacja}

write (`podaj liczbe wezlow`) ;

readln (n : 5) ;

FOR j : = 1 to 4 DO

BEGIN

A [ j ] : = 0 . 0 ;

P [ j ] ] : = 0 . 0 ;

FOR k : = 1 TO 5 DO

TAB [ j , k ] : = 0 . 0

END ;

FOR j : = 1 TO 6 DO

BEGIN

S [ j ] : = 0 . 0 ;

SUMA [ j ] : = 0 .0 ;

END ;

FOR j : = 1 TO n DO

BEGIN

write ( ` podaj wartosci x i y dla kolejnego wezla ` ) ;

readln (x:10:4, y:10:4) ;

S [ 1 ] : = x ;

FOR i : = 2 TO 6 DO S [ i ] : = x S [ i - 1 ] ;

FOR i : = 1 TO 6 DO SUMA [ i ] : = SUMA [ i ] + S [ i ] ;

P [ 1 ] : = P [ 1 ] + y ;

FOR i : = 2 TO 4 DO P [ i ] : = P [ i ] + y S [ i - 1 ]

END ;

TAB [ 1, 1 ] : = n ;

FOR i : = TO 4 DO

BEGIN

TAB [ i, 5 ] : = P [ i ] ;

FOR j : = 1 TO 4 DO

BEGIN

TAB [ i , 5 ] : = P [ i] ;

FOR j : = 1 TO 4 DO

BEGIN

k : = i + j ;

IF NOT ( k = 2 ) THEN TAB [ i , j ] : = SUMA [ k - 2 ]

END ;

END ;

RUKL ( TAB, A, 4, 5 ) ;

writeln ( ` poszukiwane wspolczynniki ` ) ;

FOR i : = 1 TO 4 DO writeln ( A [ i ] : 12 : 6 )

END.

komentarze

Przeszukaj ePrace

Copyright © 2008-2010 EPrace oraz autorzy prac.